Have you ever played with a spirograph? For those who don't know, it's a geometric drawing toy. In it's basic form, it comprises a ring and a wheel with little holes in it. To draw with it, you place the wheel inside the ring, you place a pen into one of the holes of the wheel and you move it around the inside of the ring. Here is a schema:
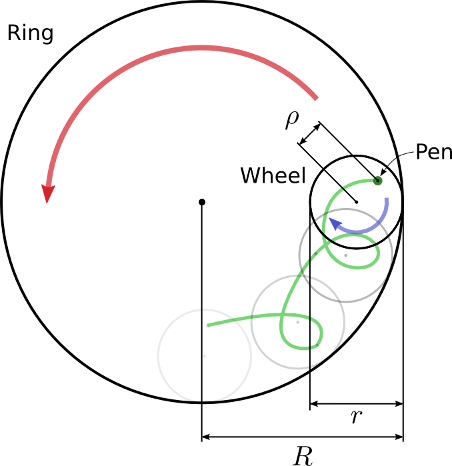
All the geometric figures produced by a spirograph can be described by the following parametric curve:
\[ x(t) = (R-r)\cos t + \rho \cos \frac{R-r}{r}t\\ y(t) = (R-r)\sin t - \rho \sin \frac{R-r}{r}t \]I made a program with openFrameworks that can draw such curves, it is available on GitHub.
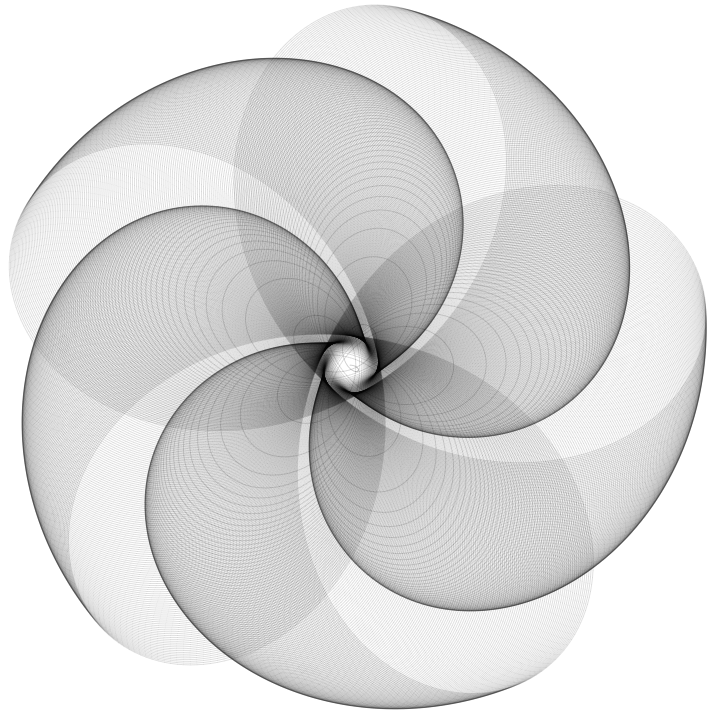
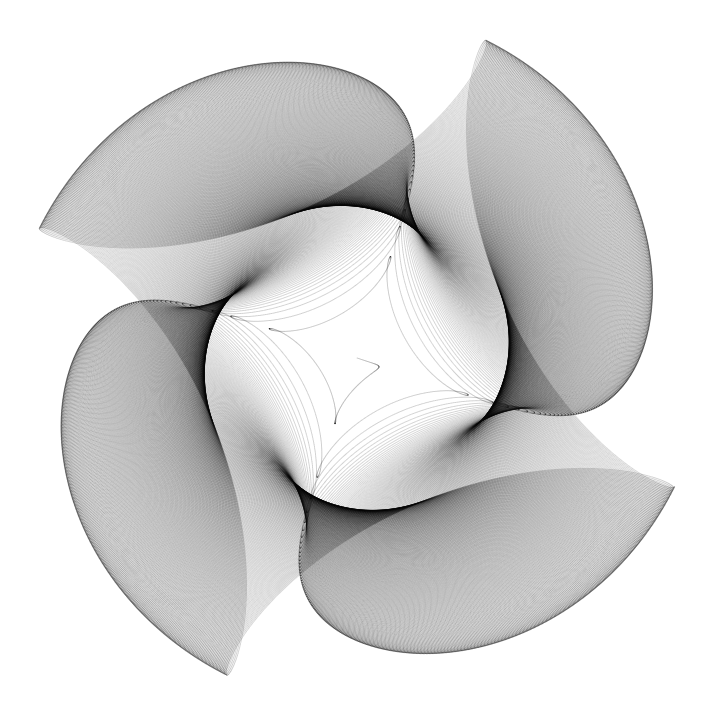
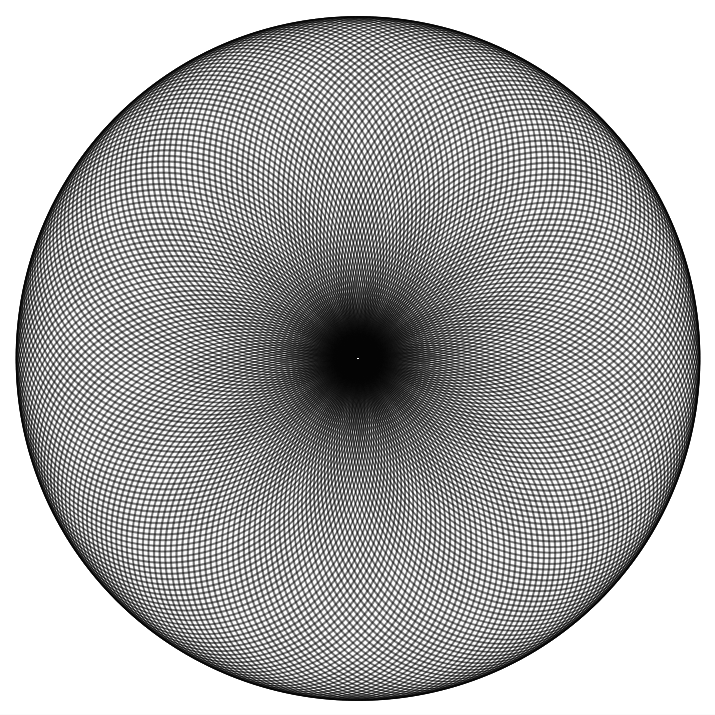
The amazing thing with this is that a very few number of parameters (3) can produce a huge variety of figures. Here are some of them:











After reading this, I added a spirality parameter. Here are some of the figures I produced using this parameter: